
Đăng ký
Bằng việc bấm đăng ký bạn đã chấp nhận các quy định sử dụng của Trường Pitago.
Thông tin mật khẩu mới đã được gửi về địa chỉ email mà bạn đăng ký.
Hãy kiểm tra email để tiếp tục!
Bạn hãy nhập câu hỏi tại đây...
Giáo viên Trần Giáp Ngọ trả lời ngày 17/09/2014.
Trả lời: 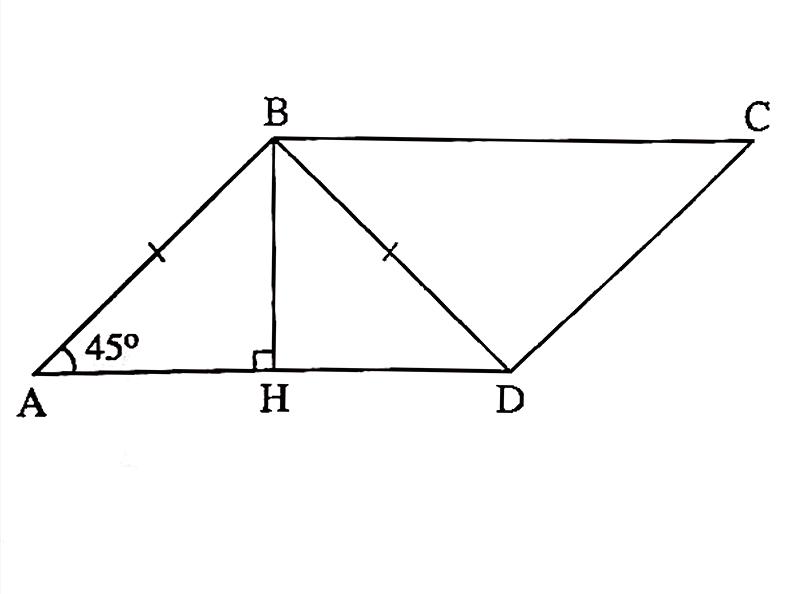
a) Kẻ \(BH \perp AD\), ta có \(AD = 2AH\)
\(BH = AB . sinA = 18 . sin45^o\)
\( = 18.\frac{\sqrt2}{2}=9\sqrt2(cm)\)
\(\triangle {AHB}\) vuông cân tại \(H\) nên ...
1 câu trả lờiBình luận
Giáo viên Dương Phúc Quân trả lời ngày 14/09/2014.
Trả lời: 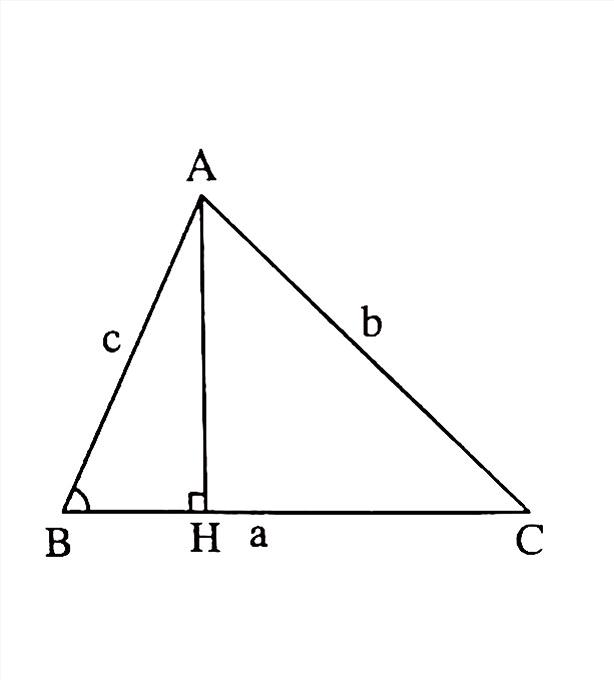
Cách 1. Tam giác \(AHC\) vuông tại \(H\), ta có:
\(AC^2 = AH^2 + HC^2\)
\(= AH^2 + (BC - HB)^2\)
\(= (AH^2 + HB^2) + BC^2 - 2BC.HB\)
...
1 câu trả lờiBình luận
Giáo viên Huỳnh Minh Chuyên trả lời ngày 05/09/2014.
Trả lời: 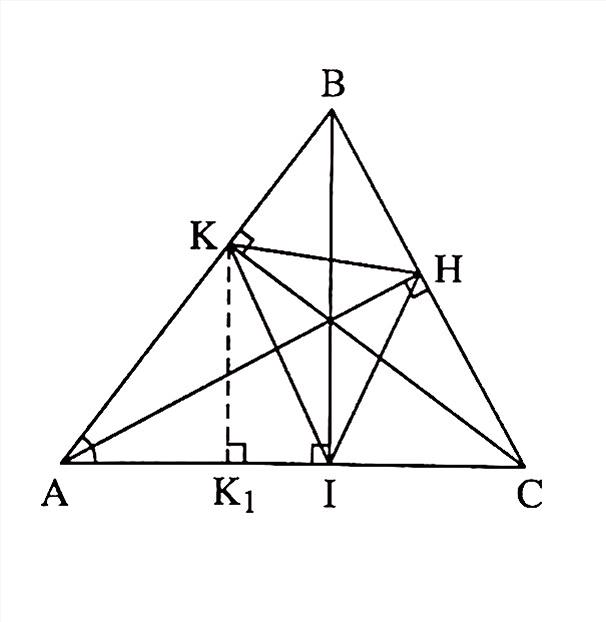
Kẻ \(KK_1 \perp AC\), ta có:
...
1 câu trả lờiBình luận
Giáo viên Phùng Lương Quyền trả lời ngày 05/09/2014.
Trả lời: 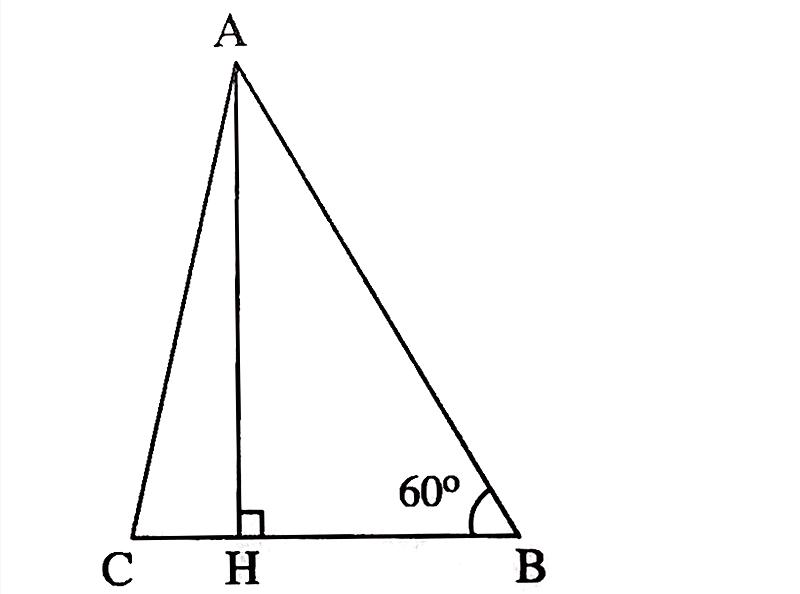
a) Kẻ đường cao \(AH\).
Xét tam giác vuông \(ABH\), ta có
\(BH = AB.cosB = AB.cos60^o = 16.\frac{1}{2}=8\)
\(AH= AB. sinB = AB.sin60^o =16.\frac{\sqrt3}{2}=8\sqrt3\)
Áp dụng đị...
1 câu trả lờiBình luận
Giáo viên Vương Đắc Mik trả lời ngày 04/09/2014.
Trả lời: Ta chứng minh:
1 câu trả lờiBình luận
Giáo viên Hà Triệu Huy trả lời ngày 03/09/2014.
Trả lời: 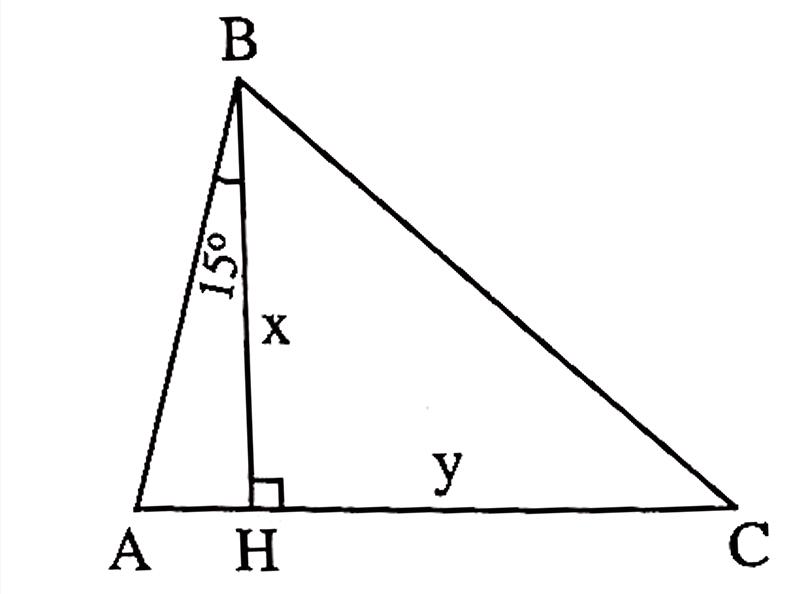
hình 2
a) (hình 1) Trước hết, ta chứng minh \(tg15^o = 2 - \sqrt3\)
Thật vậy, xét tam giác \(ABC\) vuông tại \(A\),
...
1 câu trả lờiBình luận
Giáo viên Vương Vũ Minh trả lời ngày 03/09/2014.
Trả lời: 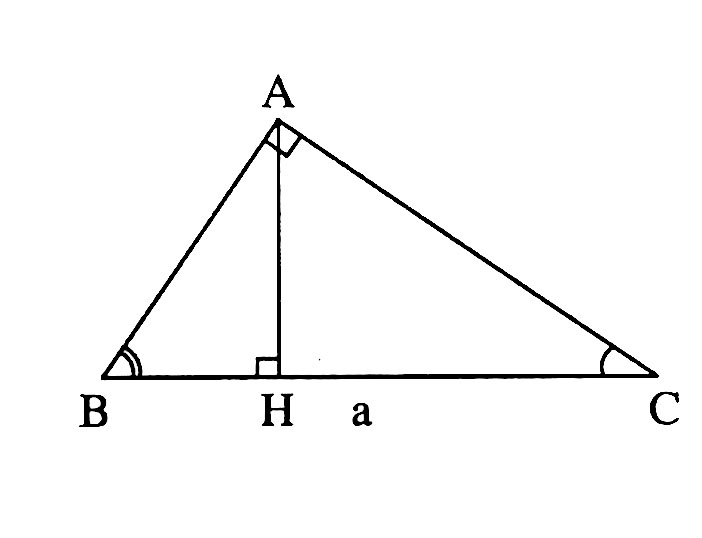
Ta có:
\(AH = ABsinB; BH = ABcosB\)
\(AB = BCcosB = acosB ; AC = BCsinB = asinB\)
Suy ra \( AH = asinBcosB\)
\(BH = a cos^2 B;\)
...
1 câu trả lờiBình luận
Giáo viên Lê Mạnh Trường trả lời ngày 01/09/2014.
Trả lời: 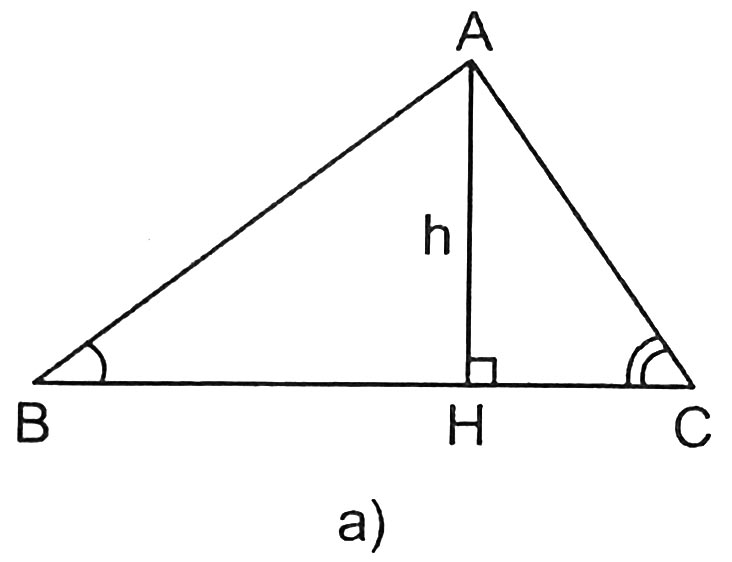
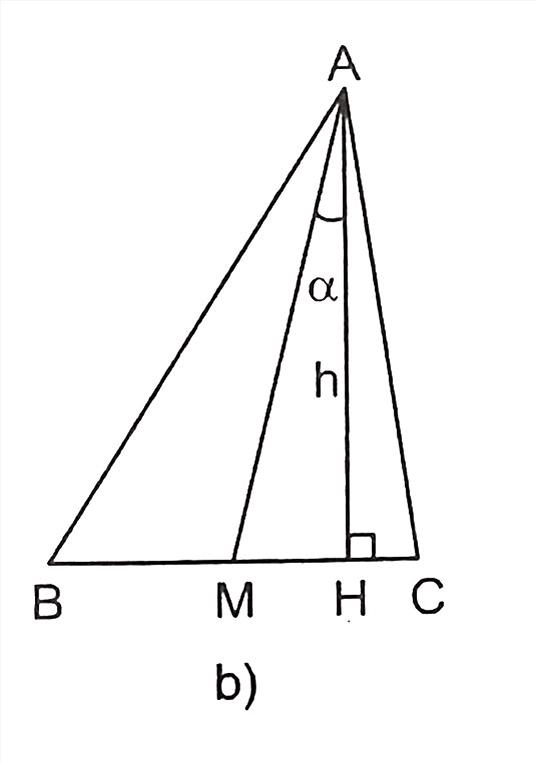
1 câu trả lờiBình luận
Giáo viên Hồ Ðông Hải trả lời ngày 30/08/2014.
Trả lời: 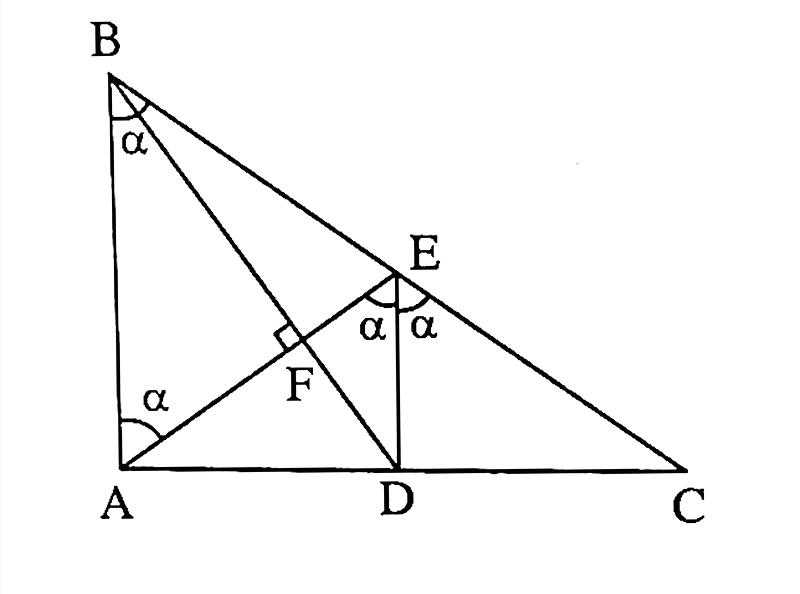
Đặt \( BE = x > 0 , \widehat {ABC} = \alpha\) thì \(EC = EA = x\) và \(\widehat {EAB} = \widehat {AED} = \widehat{DEC} = \alpha\)
Gọi giao điểm của \(AE\) và \(BD\) là \(F\).
Theo tính chất ...
1 câu trả lờiBình luận

1
312
2
Lớp 9 - THCS Đề Thám , Gia Lai
309
3
Lớp 8 - THCS Lâm Thao , Phú Thọ
292
4
Lớp 7 - THCS Cầu Giấy , Hà Nội
286
5
Lớp 9 - THCS Phú Hộ , Phú Thọ
280
6
Lớp 9 - THCS Đề Thám , Gia Lai
251
7
Lớp 9 - THCS Hoằng Châu , Thanh Hóa
243
8
Lớp 8 - THCS Nguyễn An Ninh , TP. Hồ Chí Minh
235
9
Lớp 9 - THCS Lê Ngọc Hân , Tiền Giang
218
10
Lớp 7 - Tiểu học Lê Quý Đôn , Hà Nội
192
11
Lớp 9 - THCS Lý Thái Tổ , Khánh Hòa
179
12
Lớp 6 - Tiểu học Võ Thị Sáu , Đồng Nai
168
13
Lớp 8 - Tiểu học Ninh Dân , Phú Thọ
159
14
Lớp 9 - THCS Trần Phú , Hải Phòng
157
15
Lớp 9 - THCS Nguyễn Huệ , Đà Nẵng
156
16
Lớp 9 - THCS Nguyễn Trường Tộ , Hà Nội
149
17
Lớp 9 - THCS Supe , Phú Thọ
139
18
Lớp 9 - THCS Tân Châu , Hưng Yên
136
19
Lớp 8 - Tiểu học Thị trấn Lai Vung , Đồng Tháp
134
20
Lớp 6 - Tiểu học Số 1 Mường Nhà , Điện Biên
130
 Học sinh vừa tham gia
Học sinh vừa tham gia
doran vừa tham gia Trường Pitago (2 ngày trước)
tunglam20130913 vừa tham gia Trường Pitago (2 ngày trước)
hakhathuong vừa tham gia Trường Pitago (2 ngày trước)
thuydeptraivl vừa tham gia Trường Pitago (2 ngày trước)
phuongnga1 vừa tham gia Trường Pitago (2 ngày trước)
![]() Chuyên đề liên quan
Chuyên đề liên quan
![]() Hỗ trợ học toán
Hỗ trợ học toán
SDT hỗ trợ học toán: 024-66864848 / 0964 483 669 / 0964 109 858
Email: hotro@pitago.vn
Thường trực 9h-18h, từ thứ 2 đến thứ 6
![]() Hướng dẫn
Hướng dẫn